The IMPA Model

Overview

The IMPA model is a macroeconomic policy model built on recent advances in economic theory and contemporary empirical evidence. Importantly, the model emphasizes income and wealth inequality, the prevalence of market power in labor and goods markets, productive public capital, labor market segmentation, and the nuances of the U.S. tax system.

The economy in the model is made up of three types of actors – households, firms, and the government – who interact in different markets of the economy.

The process of setting up and running a computer model of the economy as a whole is challenging. We use a programming language called Julia and implement up-to-date solution methods. We carefully match the model to data about the U.S. economy to make sure its predictions about economic impacts are as accurate as possible.

Continue reading to learn about the philosophy behind the model, as well as technical details about its construction.

Philosophy

One of the motivations behind the development of the IMPA model was the recognition of a deep disconnect between the macroeconomic models commonly used in policy debates and the more advanced frameworks found in today’s academic literature. Many policy models still rely on outdated assumptions—such as complete markets, which leave little room for public insurance or progressive taxation, and perfect competition, which renders taxation inherently distortionary by construction. While these simplifications may aid theoretical clarity, their use in applied policy models introduces a structural bias: proposals to increase tax progressivity are often dismissed not on empirical or normative grounds, but because they appear suboptimal under overly restrictive assumptions.

Market power is a clear example of this disconnect. While recent research, such as De Loecker et al. (2020) and Eeckhout (2025), has documented the widespread presence of market power across the economy, most policy models continue to ignore it. This omission leads to serious misdiagnoses. Market power alters macroeconomic behavior and shapes how firms respond to taxation, influencing aggregate investment, income and wealth distribution, and the efficiency of capital allocation. It also has direct implications for tax incidence: in an economy where firms exert pricing and wage-setting power, taxes on capital and corporate income need not be highly distortionary and can even improve allocation and reduce inequality. Ignoring market power not only distorts the theoretical lens through which we view the economy—it weakens our ability to design tax policy that reflects the economy we actually live in.

Computationally, the IMPA model is a Julia-based implementation of a large scale heterogeneous-agent, multi-sectoral, general equilibrium model of the US economy. The solution method is complex and involves very careful calibration to make economic and distributional assessments of the impact of proposed policies.

Our Model

The three types of actors in the IMPA model—households, firms, and the government—interact through markets, as illustrated in this diagram.

Diagram of the IMPA model. A description of this diagram, including The Three Types of Actors and Markets, follows this image.

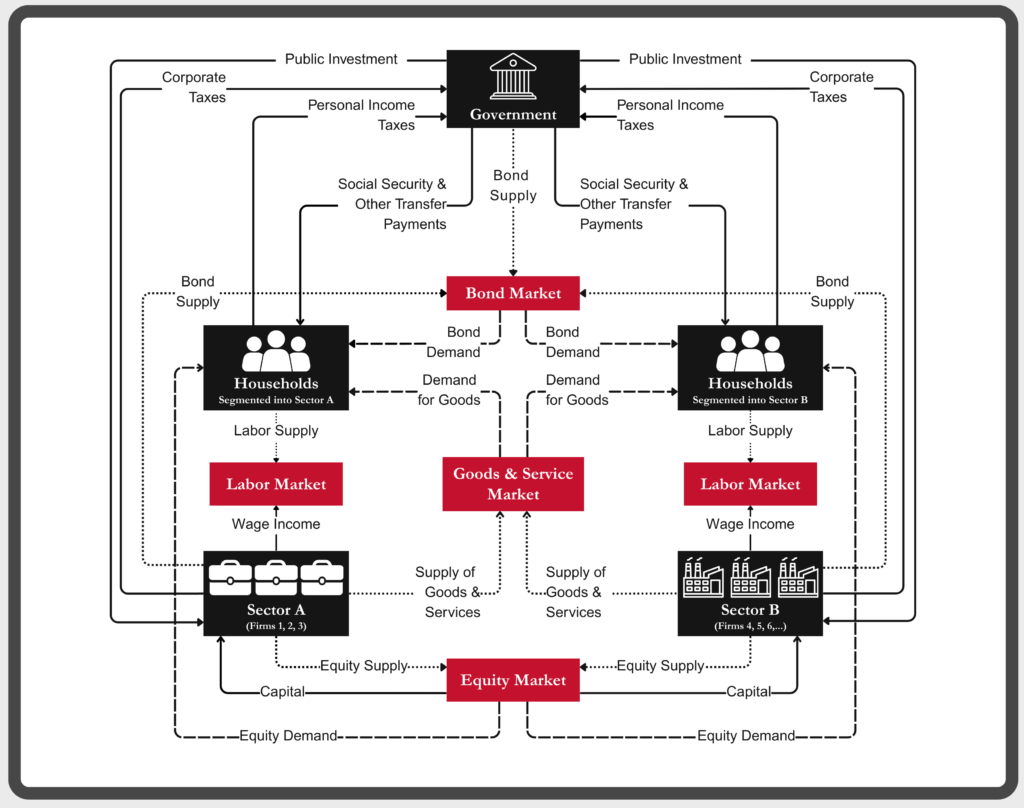
Households

The household sector comprises the workers and consumers in the economy. Households make labor supply decisions, earn income, consume goods and services, pay taxes, receive transfers, and save through liquid assets and equities. The model incorporates the following key features:

Uninsurable income risk: Households face income shocks, such as unemployment, and rely on savings to self-insure, which is consistent with the heterogeneous agent framework developed by Aiyagari (1994) and Huggett (1993, 1996) and extended by a large subsequent literature.
Multi-dimensional heterogeneity: Household decisions vary along four dimensions – age, income, employment sector, and wealth – capturing rich distributional dynamics.
Diverse income sources: Households can receive income from wages, liquid assets, capital (e.g., stock market returns), and entrepreneurial “pass-through” income.
Overlapping generations: The model includes 72 overlapping cohorts (ages 18 to 90), with retirement at age 65. Post-retirement income comes from Social Security and private savings returns.
Intergenerational linkages: Upon death, households bequeath assets to younger generations, allowing the model to capture the dynamics of wealth transmission and generational inequality.

Government

The government plays an active role in redistribution, taxation, debt issuance, and public investment. Its functions in the model include:

Taxation: The government levies a range of taxes, including payroll and social security taxes on labor income, estate taxes on bequests, dividend and capital gains taxes on capital income, and corporate taxes on firms.
Progressivity and deductions: The tax system is progressive, with rate schedules and brackets calibrated to match the tax code. Households receive standard deductions and deductions on pass-through income; firms benefit from deductions for depreciation, interest expenses, R&D, and sector-specific investment credits.
Debt issuance: The government issues bonds to finance expenditures, including Treasury bills and longer-term debt instruments.
Public investment: Government spending includes investments in infrastructure (e.g., roads, ports) and human capital (e.g., education), which enhance the productivity of private capital.

Firms

Firms operate across multiple sectors of the economy and are heterogeneous in size, productivity, and market share. They hire labor, pay wages, issue equity, produce and sell goods and services, invest in capital, and pay taxes based on their organizational form. Key features of the firm sector include:

Legal structure: Firms are classified as either corporate entities or pass-through businesses, with tax treatment varying accordingly.
Sectoral granularity: The model accommodates up to 19 distinct industries or sectors.
Monopoly power: Firms compete in oligopolistic product markets, with varying degrees of market power that allow them to influence prices, as in Atkeson and Burstein (2008).
Monopsony power: Firms possess heterogeneous wage-setting power, shaping employment conditions in local labor markets, as in Berger, Herkenhoff, and Mongey (2022).

The model follows a general equilibrium, heterogeneous-agent framework. It is solved using state-of-the-art numerical techniques drawn from the recent literature. The underlying codebase is designed with speed, flexibility, and transparency in mind. Key features include:

Implementation in Julia: The model is written entirely in Julia, an open-source language optimized for high-performance scientific computing through just-in-time (JIT) compilation.
Advanced numerical algorithms: The solution approach closely follows best practices in the literature. For example, household policy functions are computed using the endogenous grid-point method (Carroll, 2006), while transition matrices are constructed using Young’s lottery method (Young, 2010).
Sequence-space solution: The model is cast and solved in sequence space (Auclert et al., 2021), significantly accelerating the computation of equilibria. To handle large, discrete policy changes – such as the Tax Cuts and Jobs Act (TCJA) – we implement a Newton-Raphson solution method following Boehm (2024).
Modular code design: The architecture separates solution routines from model-specific features, allowing for flexibility across applications – e.g., toggling between single- and multi-sector economies, or switching between corporate and pass-through firm structures.
Radical transparency: The entire codebase is developed on GitHub. While the repository is currently private (pending completion of the testing suite), it will be made public to encourage reuse, modification, and extension by researchers and practitioners.

An academic exposition of the IMPA model can be found in the paper Brun, Gonzalez, and Montecino (2023). Some of the mechanisms of the IMPA model are explored in Gonzalez, Montecino, and Stiglitz (2025).

References

Aiyagari, S. R. (1994). Uninsured Idiosyncratic Risk and Aggregate Saving. Quarterly Journal of Economics, 109(3), 659–684.

Atkeson, A., & Burstein, A. T. (2008). Pricing-to-Market, Trade Costs, and International Relative Prices. American Economic Review, 98(5), 1998–2031.

Auclert, A., Bardóczy, B., Rognlie, M., & Straub, L. (2021). Using the Sequence‐Space Jacobian to Solve and Estimate Heterogeneous‐agent Models. Econometrica, 89(5), 2375-2408.

Berger, D. W., Herkenhoff, K. F., & Mongey, S. (2022). Labor Market Power. American Economic Review, 112(11), 3534–3568.

Boehl, G. (2023). HANK on Speed: Robust Nonlinear Solutions using Automatic Differentiation. Available at SSRN 4433585.

Brun, L., González, I., & Montecino, J. (2023). Corporate Taxation and Market Power Wealth. Available at SSRN.

Carroll, C. D. (2006). The Method of Endogenous Gridpoints for Solving Dynamic Stochastic Optimization Problems. Economics Letters, 91(3), 312-320.

De Loecker, Jan, Jan Eeckhout, and Gabriel Unger. (2020). The Rise of Market Power and the Macroeconomic Implications. The Quarterly Journal of Economics, 135(2), 561–644.

Eeckhout, Jan. (2025). Presidential Address 2024: The Value and Profits of Firms. Journal of the European Economic Association, 23(1), 52–118.

González, I., Montecino, J. A., & Stiglitz, J. E. (2025). Equity Prices, Market Power, and Optimal Corporate Tax Policy. NBER Working Paper No. 33544.

Huggett, M. (1993). The Risk-Free Rate in Heterogeneous-Agent Incomplete-Insurance Economies. Journal of Economic Dynamics and Control, 17(5–6), 953–969.

Huggett, M. (1996). Wealth Distribution in Life-Cycle Economies. Journal of Monetary Economics, 38(3), 469–494.

Young, E. R. (2010). Solving the Incomplete Markets Model with Aggregate Uncertainty Using the Krusell–Smith Algorithm and Non-stochastic Simulations. Journal of Economic Dynamics and Control, 34(1), 36-41.